Create an object of the ALE statistics of a random variable that can be used to generate p-values

ALE statistics are accompanied with two indicators of the confidence of their values. First, bootstrapping creates confidence intervals for ALE measures and ALE statistics to give a range of the possible likely values. Second, we calculate p-values, an indicator of the probability that a given ALE statistic is random. Calculating p-values is not trivial for ALE statistics because ALE is non-parametric and model-agnostic. Because ALE is non-parametric (that is, it does not assume any particular distribution of data), the ale package generates p-values by calculating ALE for many random variables; this makes the procedure somewhat slow. For this reason, they are not calculated by default; they must be explicitly requested. Because the ale package is model-agnostic (that is, it works with any kind of R model), the ale() function cannot always automatically manipulate the model object to create the p-values. It can only do so for models that follow the standard R statistical modelling conventions, which includes almost all built-in R algorithms (like stats::lm() and stats::glm()) and many widely used statistics packages (like mgcv and survival), but which excludes most machine learning algorithms (like tidymodels and caret). For non-standard algorithms, the user needs to do a little work to help the ale function correctly manipulate its model object:

The full model call must be passed as a character string in the argument 'random_model_call_string', with two slight modifications as follows.
In the formula that specifies the model, you must add a variable named 'random_variable'. This corresponds to the random variables that create_p_dist() will use to estimate p-values.
The dataset on which the model is trained must be named 'rand_data'. This corresponds to the modified datasets that will be used to train the random variables.

See the example below for how this is implemented.

Usage

create_p_dist(
  data,
  model,
  p_speed = "approx fast",
  ...,
  parallel = future::availableCores(logical = FALSE, omit = 1),
  model_packages = NULL,
  random_model_call_string = NULL,
  random_model_call_string_vars = character(),
  y_col = NULL,
  binary_true_value = TRUE,
  pred_fun = function(object, newdata, type = pred_type) {
     stats::predict(object =
    object, newdata = newdata, type = type)
 },
  pred_type = "response",
  output = NULL,
  rand_it = 1000,
  seed = 0,
  silent = FALSE,
  .testing_mode = FALSE
)

Arguments

data: See documentation for ale()
model: See documentation for ale()
p_speed: character(1). Either 'approx fast' (default) or 'precise slow'. See details.
...: not used. Inserted to require explicit naming of subsequent arguments.
parallel: See documentation for ale()
model_packages: See documentation for ale()
random_model_call_string: character string. If NULL, create_p_dist() tries to automatically detect and construct the call for p-values. If it cannot, the function will fail early. In that case, a character string of the full call for the model must be provided that includes the random variable. See details.
random_model_call_string_vars: See documentation for model_call_string_vars in model_bootstrap(); their operation is very similar.
y_col: See documentation for ale()
binary_true_value: See documentation for model_bootstrap()
pred_fun, pred_type: See documentation for ale().
output: character string. If 'residuals', returns the residuals in addition to the raw data of the generated random statistics (which are always returned). If NULL (default), does not return the residuals.
rand_it: non-negative integer length 1. Number of times that the model should be retrained with a new random variable. The default of 1000 should give reasonably stable p-values. It can be reduced as low as 100 for faster test runs.
seed: See documentation for ale()
silent: See documentation for ale()
.testing_mode: logical(1). Internal use only. Disables some data validation checks to allow for debugging.

Value

The return value is an object of class ale_p. See examples for an illustration of how to inspect this list. Its elements are:

rand_stats: A named list of tibbles. There is normally one element whose name is the same as y_col except if y_col is a categorical variable; in that case, the elements are named for each category of y_col. Each element is a tibble whose rows are each of the rand_it_ok iterations of the random variable analysis and whose columns are the ALE statistics obtained for each random variable.
residual_distribution: A univariateML object with the closest estimated distribution for the residuals as determined by univariateML::model_select(). This is the distribution used to generate all the random variables.
rand_it_ok: An integer with the number of rand_it iterations that successfully generated a random variable, that is, those that did not fail for whatever reason. The rand_it - rand_it_ok failed attempts are discarded.
residuals: If output = 'residuals', returns a matrix of the actual y_col values from data minus the predicted values from the model (without random variables) on the data. If output = NULL, (default), does not return these residuals. The rows correspond to each row of data. The columns correspond to the named elements described above for rand_stats.

Approach to calculating p-values

The ale package takes a literal frequentist approach to the calculation of p-values. That is, it literally retrains the model 1000 times, each time modifying it by adding a distinct random variable to the model. (The number of iterations is customizable with the rand_it argument.) The ALEs and ALE statistics are calculated for each random variable. The percentiles of the distribution of these random-variable ALEs are then used to determine p-values for non-random variables. Thus, p-values are interpreted as the frequency of random variable ALE statistics that exceed the value of ALE statistic of the actual variable in question. The specific steps are as follows:

The residuals of the original model trained on the training data are calculated (residuals are the actual y target value minus the predicted values).
The closest distribution of the residuals is detected with univariateML::model_select().
1000 new models are trained by generating a random variable each time with univariateML::rml() and then training a new model with that random variable added.
The ALEs and ALE statistics are calculated for each random variable.
For each ALE statistic, the empirical cumulative distribution function (from stats::ecdf()) is used to create a function to determine p-values according to the distribution of the random variables' ALE statistics.

What we have just described is the precise approach to calculating p-values with the argument p_speed = 'precise slow'. Because it is so slow, by default, create_p_dist() implements an approximate algorithm by default (p_speed = 'approx fast') which trains only a few random variables up to the number of physical parallel processing threads available, with a minimum of four. To increase speed, the random variable uses only 10 ALE bins instead of the default 100. Although approximate p-values are much faster than precise ones, they are still somewhat slow: at the very quickest, they take at least the amount of time that it would take to train the original model two or three times. See the "Parallel processing" section below for more details on the speed of computation.

Parallel processing

Parallel processing using the {furrr} framework is enabled by default. By default, it will use all the available physical CPU cores (minus the core being used for the current R session) with the setting parallel = future::availableCores(logical = FALSE, omit = 1). Note that only physical cores are used (not logical cores or "hyperthreading") because machine learning can only take advantage of the floating point processors on physical cores, which are absent from logical cores. Trying to use logical cores will not speed up processing and might actually slow it down with useless data transfer.

For exact p-values, by default 1000 random variables are trained. So, even with parallel processing, the procedure is very slow. However, an ale_p object trained with a specific model on a specific dataset can be reused as often as needed for the identical model-dataset pair.

For approximate p-values (the default), at least four random variables are trained to give some minimal variation. With parallel processing, more random variables can be trained to increase the accuracy of the p_value estimates up to the maximum number of physical cores.

References

Okoli, Chitu. 2023. “Statistical Inference Using Machine Learning and Classical Techniques Based on Accumulated Local Effects (ALE).” arXiv. https://arxiv.org/abs/2310.09877.

Examples

# \donttest{
# Sample 1000 rows from the ggplot2::diamonds dataset (for a simple example)
set.seed(0)
diamonds_sample <- ggplot2::diamonds[sample(nrow(ggplot2::diamonds), 1000), ]

# Create a GAM with flexible curves to predict diamond price
# Smooth all numeric variables and include all other variables
gam_diamonds <- mgcv::gam(
  price ~ s(carat) + s(depth) + s(table) + s(x) + s(y) + s(z) +
    cut + color + clarity,
  data = diamonds_sample
)
summary(gam_diamonds)
#> 
#> Family: gaussian 
#> Link function: identity 
#> 
#> Formula:
#> price ~ s(carat) + s(depth) + s(table) + s(x) + s(y) + s(z) + 
#>     cut + color + clarity
#> 
#> Parametric coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  3421.412     74.903  45.678  < 2e-16 ***
#> cut.L         261.339    171.630   1.523 0.128170    
#> cut.Q          53.684    129.990   0.413 0.679710    
#> cut.C         -71.942    103.804  -0.693 0.488447    
#> cut^4          -8.657     80.614  -0.107 0.914506    
#> color.L     -1778.903    113.669 -15.650  < 2e-16 ***
#> color.Q      -482.225    104.675  -4.607 4.64e-06 ***
#> color.C        58.724     95.983   0.612 0.540807    
#> color^4       125.640     87.111   1.442 0.149548    
#> color^5      -241.194     81.913  -2.945 0.003314 ** 
#> color^6       -49.305     74.435  -0.662 0.507883    
#> clarity.L    4141.841    226.713  18.269  < 2e-16 ***
#> clarity.Q   -2367.820    217.185 -10.902  < 2e-16 ***
#> clarity.C    1026.214    180.295   5.692 1.67e-08 ***
#> clarity^4    -602.066    137.258  -4.386 1.28e-05 ***
#> clarity^5     408.336    105.344   3.876 0.000113 ***
#> clarity^6     -82.379     88.434  -0.932 0.351815    
#> clarity^7       4.017     78.816   0.051 0.959362    
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Approximate significance of smooth terms:
#>            edf Ref.df      F  p-value    
#> s(carat) 7.503  8.536  4.114 3.65e-05 ***
#> s(depth) 1.486  1.874  0.601 0.614753    
#> s(table) 2.929  3.738  1.294 0.240011    
#> s(x)     8.897  8.967  3.323 0.000542 ***
#> s(y)     3.875  5.118 11.075  < 2e-16 ***
#> s(z)     9.000  9.000  2.648 0.004938 ** 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> R-sq.(adj) =   0.94   Deviance explained = 94.3%
#> GCV = 9.7669e+05  Scale est. = 9.262e+05  n = 1000

# Create p_value distribution
pd_diamonds <- create_p_dist(
  diamonds_sample,
  gam_diamonds,
  # only 100 iterations for a quick demo; but usually should remain at 1000
  rand_it = 100,
)

# Examine the structure of the returned object
str(pd_diamonds)
#> List of 3
#>  $ rand_stats           :List of 1
#>   ..$ price: tibble [4 × 6] (S3: tbl_df/tbl/data.frame)
#>   .. ..$ aled     : num [1:4] 49.1 48.8 51 15.6
#>   .. ..$ aler_min : num [1:4] -255.6 -309.2 -95.2 -75.7
#>   .. ..$ aler_max : num [1:4] 365 384 460 103
#>   .. ..$ naled    : num [1:4] 0.545 0.546 0.533 0.211
#>   .. ..$ naler_min: num [1:4] -3 -3.8 -0.8 -0.7
#>   .. ..$ naler_max: num [1:4] 3.4 3.6 4.4 1.2
#>  $ residual_distribution: 'univariateML' Named num [1:4] 9.08 1052.62 2.88 1.25
#>   ..- attr(*, "names")= chr [1:4] "mean" "sd" "nu" "xi"
#>   ..- attr(*, "model")= chr "Skew Student-t"
#>   ..- attr(*, "density")= chr "fGarch::dsstd"
#>   ..- attr(*, "logLik")= num -8123
#>   ..- attr(*, "support")= num [1:2] -Inf Inf
#>   ..- attr(*, "n")= int 1000
#>   ..- attr(*, "call")= language f(x = x, na.rm = na.rm)
#>  $ rand_it_ok           : int 4
#>  - attr(*, "class")= chr "ale_p"
# In RStudio: View(pd_diamonds)

# Calculate ALEs with p-values
ale_gam_diamonds <- ale(
  diamonds_sample,
  gam_diamonds,
  p_values = pd_diamonds
)

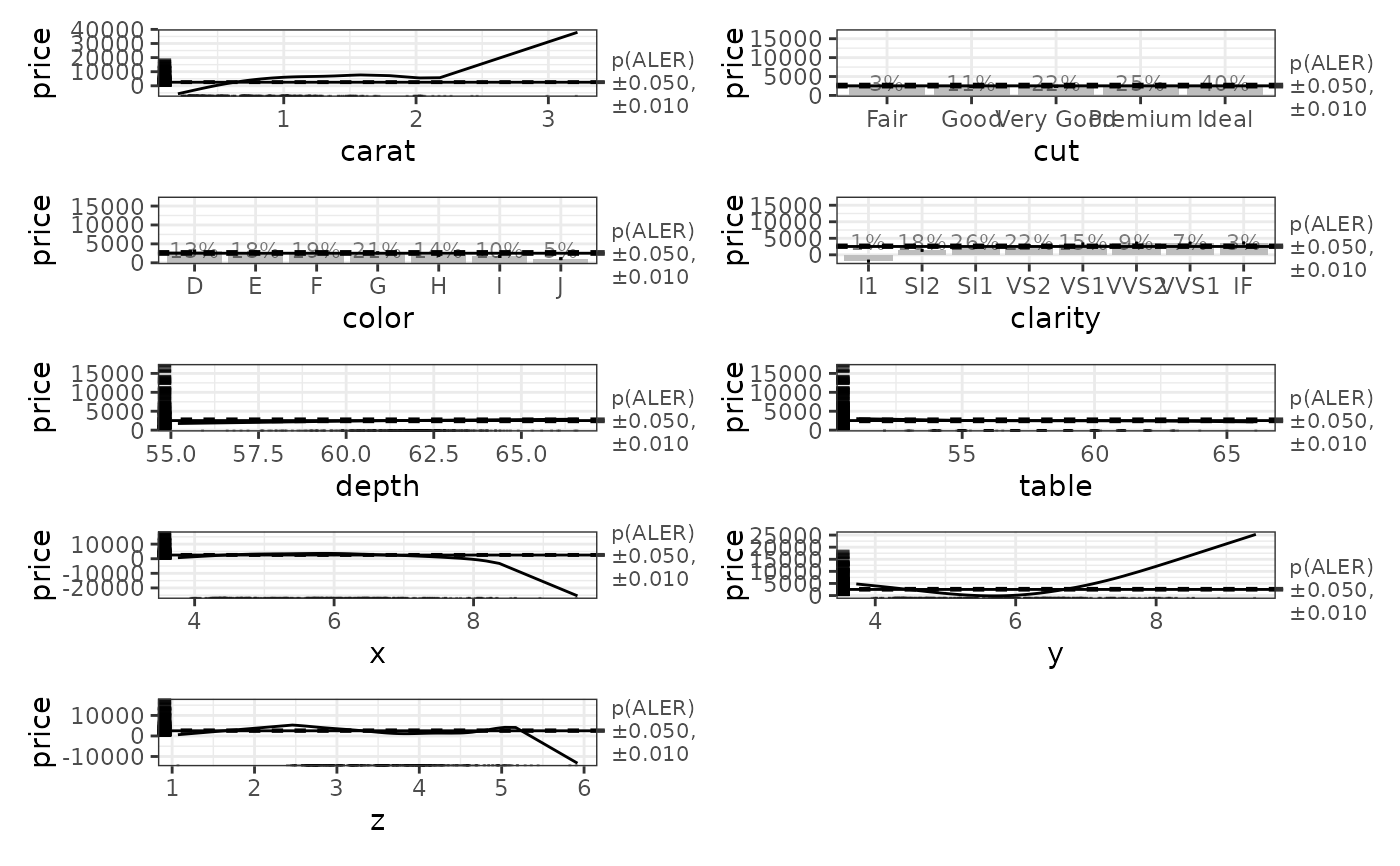
# Plot the ALE data. The horizontal bands in the plots use the p-values.
diamonds_plots <- plot(ale_gam_diamonds)
diamonds_1D_plots <- diamonds_plots$distinct$price$plots[[1]]
patchwork::wrap_plots(diamonds_1D_plots, ncol = 2)



# For non-standard models that give errors with the default settings,
# you can use 'random_model_call_string' to specify a model for the estimation
# of p-values from random variables as in this example.
# See details above for an explanation.
pd_diamonds <- create_p_dist(
  diamonds_sample,
  gam_diamonds,
  random_model_call_string = 'mgcv::gam(
    price ~ s(carat) + s(depth) + s(table) + s(x) + s(y) + s(z) +
        cut + color + clarity + random_variable,
    data = rand_data
  )',
  # only 100 iterations for a quick demo; but usually should remain at 1000
  rand_it = 100,
)

# }