Introduction to the ale package
Chitu Okoli
October 24, 2023
Source:vignettes/ale-intro.Rmd
ale-intro.RmdAccumulated Local Effects (ALE) were initially developed as a model-agnostic
approach for global explanations of the results of black-box machine
learning algorithms. ALE has at least two primary advantages over
other approaches like partial dependency plots (PDP) and SHapley
Additive exPlanations (SHAP): its values are not affected by the
presence of interactions among variables in a model and its computation
is relatively rapid. This package rewrites the original code from the {ALEPlot}
package for calculating ALE data and it completely reimplements the
plotting of ALE values. It also extends the original ALE concept to add
bootstrap-based confidence intervals and ALE-based statistics that can
be used for statistical inference.
For more details, see Okoli, Chitu. 2023. “Statistical Inference Using Machine Learning and Classical Techniques Based on Accumulated Local Effects (ALE).” arXiv. https://doi.org/10.48550/arXiv.2310.09877.
This vignette demonstrates the basic functionality of the
ale package on standard large datasets used for machine
learning. A separate vignette is devoted to its use on small datasets, as is often
the case with statistical inference. (How small is small? That’s a tough
question, but as that vignette explains, most datasets of less than 2000
rows are probably “small” and even many datasets that are more than 2000
rows are nonetheless “small”.) Other vignettes introduce ALE-based statistics for statistical
inference, show how the ale package handles various datatypes of input variables,
and compares
the {ale} package with the reference {ALEPlot}
package.
We begin by loading the necessary libraries.
library(ale)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, uniondiamonds dataset
For this introduction, we use the diamonds dataset,
included with the ggplot2 graphics system. We cleaned the
original version by removing duplicates and
invalid entries where the length (x), width (y), or depth (z) is 0.
# Clean up some invalid entries
diamonds <- ggplot2::diamonds |>
filter(!(x == 0 | y == 0 | z == 0)) |>
# https://lorentzen.ch/index.php/2021/04/16/a-curious-fact-on-the-diamonds-dataset/
distinct(
price, carat, cut, color, clarity,
.keep_all = TRUE
) |>
rename(
x_length = x,
y_width = y,
z_depth = z,
depth_pct = depth
)
# Optional: sample 1000 rows so that the code executes faster.
set.seed(0)
diamonds_sample <- ggplot2::diamonds[sample(nrow(ggplot2::diamonds), 1000), ]
summary(diamonds)
#> carat cut color clarity depth_pct
#> Min. :0.2000 Fair : 1492 D:4658 SI1 :9857 Min. :43.00
#> 1st Qu.:0.5200 Good : 4173 E:6684 VS2 :8227 1st Qu.:61.00
#> Median :0.8500 Very Good: 9714 F:6998 SI2 :7916 Median :61.80
#> Mean :0.9033 Premium : 9657 G:7815 VS1 :6007 Mean :61.74
#> 3rd Qu.:1.1500 Ideal :14703 H:6443 VVS2 :3463 3rd Qu.:62.60
#> Max. :5.0100 I:4556 VVS1 :2413 Max. :79.00
#> J:2585 (Other):1856
#> table price x_length y_width
#> Min. :43.00 Min. : 326 Min. : 3.730 Min. : 3.680
#> 1st Qu.:56.00 1st Qu.: 1410 1st Qu.: 5.160 1st Qu.: 5.170
#> Median :57.00 Median : 3365 Median : 6.040 Median : 6.040
#> Mean :57.58 Mean : 4686 Mean : 6.009 Mean : 6.012
#> 3rd Qu.:59.00 3rd Qu.: 6406 3rd Qu.: 6.730 3rd Qu.: 6.720
#> Max. :95.00 Max. :18823 Max. :10.740 Max. :58.900
#>
#> z_depth
#> Min. : 1.070
#> 1st Qu.: 3.190
#> Median : 3.740
#> Mean : 3.711
#> 3rd Qu.: 4.150
#> Max. :31.800
#> Here is the description of the modified dataset.
| Variable | Description |
|---|---|
| price | price in US dollars ($326–$18,823) |
| carat | weight of the diamond (0.2–5.01) |
| cut | quality of the cut (Fair, Good, Very Good, Premium, Ideal) |
| color | diamond color, from D (best) to J (worst) |
| clarity | a measurement of how clear the diamond is (I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best)) |
| x_length | length in mm (0–10.74) |
| y_width | width in mm (0–58.9) |
| z_depth | depth in mm (0–31.8) |
| depth_pct | total depth percentage = z / mean(x, y) = 2 * z / (x + y) (43–79) |
| table | width of top of diamond relative to widest point (43–95) |
str(diamonds)
#> tibble [39,739 × 10] (S3: tbl_df/tbl/data.frame)
#> $ carat : num [1:39739] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...
#> $ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ...
#> $ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ...
#> $ clarity : Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ...
#> $ depth_pct: num [1:39739] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...
#> $ table : num [1:39739] 55 61 65 58 58 57 57 55 61 61 ...
#> $ price : int [1:39739] 326 326 327 334 335 336 336 337 337 338 ...
#> $ x_length : num [1:39739] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...
#> $ y_width : num [1:39739] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...
#> $ z_depth : num [1:39739] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...
summary(diamonds$price)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 326 1410 3365 4686 6406 18823Interpretable machine learning (IML) techniques like ALE should be applied not on training subsets nor on test subsets but on a final deployment model after training and evaluation. This final deployment should be trained on the full dataset to give the best possible model for production deployment. (When a dataset is too small to feasibly split into training and test sets, then the ale package has tools to appropriately handle such small datasets.
Modelling with general additive models (GAM)
ALE is a model-agnostic IML approach, that is, it works with any kind of machine learning model. As such, ale works with any R model with the only condition that it can predict numeric outcomes (such as raw estimates for regression and probabilities or odds ratios for classification). For this demonstration, we will use general additive models (GAM), a relatively fast algorithm that models data more flexibly than ordinary least squares regression. It is beyond our scope here to explain how GAM works (you can learn more with Noam Ross’s excellent tutorial), but the examples here will work with any machine learning algorithm.
We train a GAM model to predict diamond prices:
# Create a GAM model with flexible curves to predict diamond prices.
# (In testing, mgcv::gam actually performed better than nnet.)
# Smooth all numeric variables and include all other variables.
gam_diamonds <- mgcv::gam(
price ~ s(carat) + s(depth_pct) + s(table) + s(x_length) + s(y_width) + s(z_depth) +
cut + color + clarity,
data = diamonds
)
summary(gam_diamonds)
#>
#> Family: gaussian
#> Link function: identity
#>
#> Formula:
#> price ~ s(carat) + s(depth_pct) + s(table) + s(x_length) + s(y_width) +
#> s(z_depth) + cut + color + clarity
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4436.199 13.315 333.165 < 2e-16 ***
#> cut.L 263.124 39.117 6.727 1.76e-11 ***
#> cut.Q 1.792 27.558 0.065 0.948151
#> cut.C 74.074 20.169 3.673 0.000240 ***
#> cut^4 27.694 14.373 1.927 0.054004 .
#> color.L -2152.488 18.996 -113.313 < 2e-16 ***
#> color.Q -704.604 17.385 -40.528 < 2e-16 ***
#> color.C -66.839 16.366 -4.084 4.43e-05 ***
#> color^4 80.376 15.289 5.257 1.47e-07 ***
#> color^5 -110.164 14.484 -7.606 2.89e-14 ***
#> color^6 -49.565 13.464 -3.681 0.000232 ***
#> clarity.L 4111.691 33.499 122.742 < 2e-16 ***
#> clarity.Q -1539.959 31.211 -49.341 < 2e-16 ***
#> clarity.C 762.680 27.013 28.234 < 2e-16 ***
#> clarity^4 -232.214 21.977 -10.566 < 2e-16 ***
#> clarity^5 193.854 18.324 10.579 < 2e-16 ***
#> clarity^6 46.812 16.172 2.895 0.003799 **
#> clarity^7 132.621 14.274 9.291 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(carat) 8.695 8.949 37.027 < 2e-16 ***
#> s(depth_pct) 7.606 8.429 6.758 < 2e-16 ***
#> s(table) 5.759 6.856 3.682 0.000736 ***
#> s(x_length) 8.078 8.527 60.936 < 2e-16 ***
#> s(y_width) 7.477 8.144 211.202 < 2e-16 ***
#> s(z_depth) 9.000 9.000 16.266 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.929 Deviance explained = 92.9%
#> GCV = 1.2602e+06 Scale est. = 1.2581e+06 n = 39739Enable progress bars
Before starting, we recommend that you enable progress bars to see how long procedures will take. Simply run the following code at the beginning of your R session:
# Run this in an R console; it will not work directly within an R Markdown or Quarto block
progressr::handlers(global = TRUE)
progressr::handlers('cli')If you forget to do that, the ale package will do it automatically for you with a notification message.
ale() function for generating ALE data and plots
The core function in the ale package is the
ale() function. Consistent with tidyverse conventions, its
first argument is a dataset. Its second argument is a model object–any R
model object that can generate numeric predictions is acceptable. By
default, it generates ALE data and plots on all the input variables used
for the model. To change these options (e.g., to calculate ALE for only
a subset of variables; to output the data only or the plots only rather
than both; or to use a custom, non-standard predict function for the
model), see details in the help file for the function:
help(ale).
The ale() function returns a list with various elements.
The two main ones are data, containing the ALE x intervals
and the y values for each interval, and plots, containing
the ALE plots as individual ggplot objects. Each of these
elements is a list with one element per input variable. The function
also returns several details about the outcome (y) variable and
important parameters that were used for the ALE calculation. Another
important element is stats, containing ALE-based
statistics, which we describe in a separate vignette.
# Simple ALE without bootstrapping
ale_gam_diamonds <- ale(
diamonds, gam_diamonds,
parallel = 2 # CRAN limit (delete this line on your own computer)
)By default, most core functions in the ale package use
parallel processing. However, this requires explicit specification of
the packages used to build the model, specified with the
model_packages argument. (If parallelization is disabled
with parallel = 0, then model_packages is not
required.) See help(ale) for more details.
To access the plot for a specific variable, we must first create an
ale_plots object by calling the plot() method on the
ale object which generates ggplot objects with
the full flexibility of {ggplot2}:
# Print a plot by entering its reference
diamonds_plots <- plot(ale_gam_diamonds)The plots object is somewhat complex, so it is easier to work with by
using the following code to simplify it. (A future version of the ale
package should simplify working directly with ale_plots
objects.)
# Extract one-way ALE plots from the ale_plots object
diamonds_1D_plots <- diamonds_plots$distinct$price$plots[[1]]The diamonds_1D_plots object is now simply a list of all the 1D ALE
plots. The desired variable plot can now be easily plotted by printing
its reference by name. For example, to access and print the
carat ALE plot, we simply refer to
diamonds_1D_plots$carat:
# Print a plot by entering its reference
diamonds_1D_plots$carat
To iterate the list and plot all the ALE plots, we can use the
patchwork package to arrange multiple plots in a common
plot grid using patchwork::wrap_plots(). We need to pass
the list of plots to the grobs argument and we can specify
that we want two plots per row with the ncol argument.
# Print all plots
patchwork::wrap_plots(diamonds_1D_plots, ncol = 2)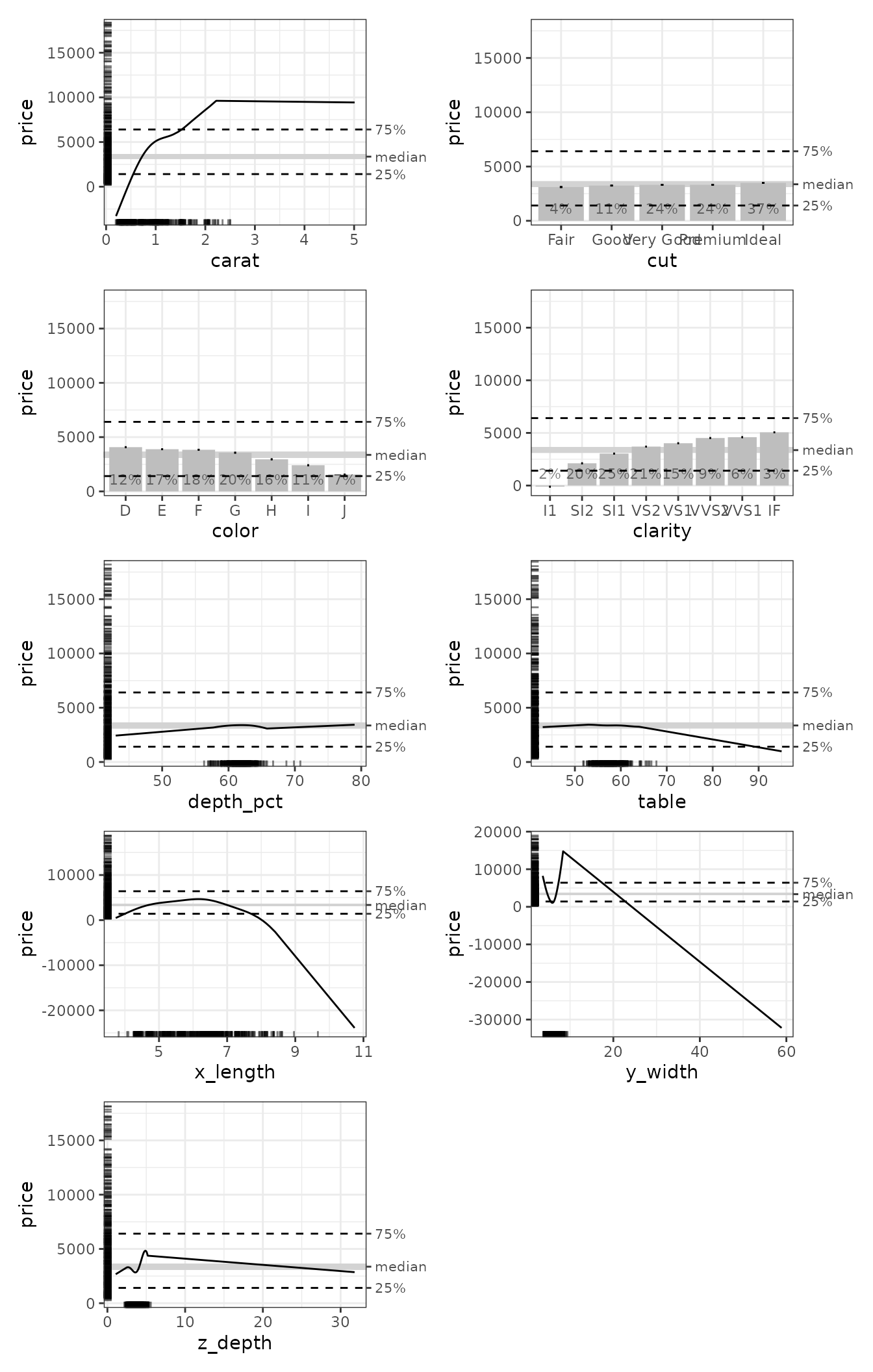
Bootstrapped ALE
One of the key features of the ALE package is bootstrapping of the
ALE results to ensure that the results are reliable, that is,
generalizable to data beyond the sample on which the model was built. As
mentioned above, this assumes that IML analysis is carried out on a
final deployment model selected after training and evaluating the model
hyperparameters on distinct subsets. When samples are too small for
this, we provide a different bootstrapping method,
model_bootstrap(), explained in the vignette for small datasets.
Although ALE is faster than most other IML techniques for global explanation such as partial dependence plots (PDP) and SHAP, it still requires some time to run. Bootstrapping multiplies that time by the number of bootstrap iterations. Since this vignette is just a demonstration of package functionality rather than a real analysis, we will demonstrate bootstrapping on a small subset of the test data. This will run much faster as the speed of the ALE algorithm depends on the size of the dataset. So, let us take a random sample of 200 rows of the test set.
# Bootstraping is rather slow, so create a smaller subset of new data for demonstration
set.seed(0)
new_rows <- sample(nrow(diamonds), 200, replace = FALSE)
diamonds_small_test <- diamonds[new_rows, ]Now we create bootstrapped ALE data and plots using the
boot_it argument. ALE is a relatively stable IML algorithm
(compared to others like PDP), so 100 bootstrap samples should be
sufficient for relatively stable results, especially for model
development. Final results could be confirmed with 1000 bootstrap
samples or more, but there should not be much difference in the results
beyond 100 iterations. However, so that this introduction runs faster,
we demonstrate it here with only 10 iterations.
ale_gam_diamonds_boot <- ale(
diamonds_small_test, gam_diamonds,
# Normally boot_it should be set to 100, but just 10 here for a faster demonstration
boot_it = 10,
parallel = 2 # CRAN limit (delete this line on your own computer)
)
# Bootstrapping produces confidence intervals
boot_plots <- plot(ale_gam_diamonds_boot)
boot_1D_plots <- boot_plots$distinct$price$plots[[1]]
patchwork::wrap_plots(boot_1D_plots, ncol = 2)
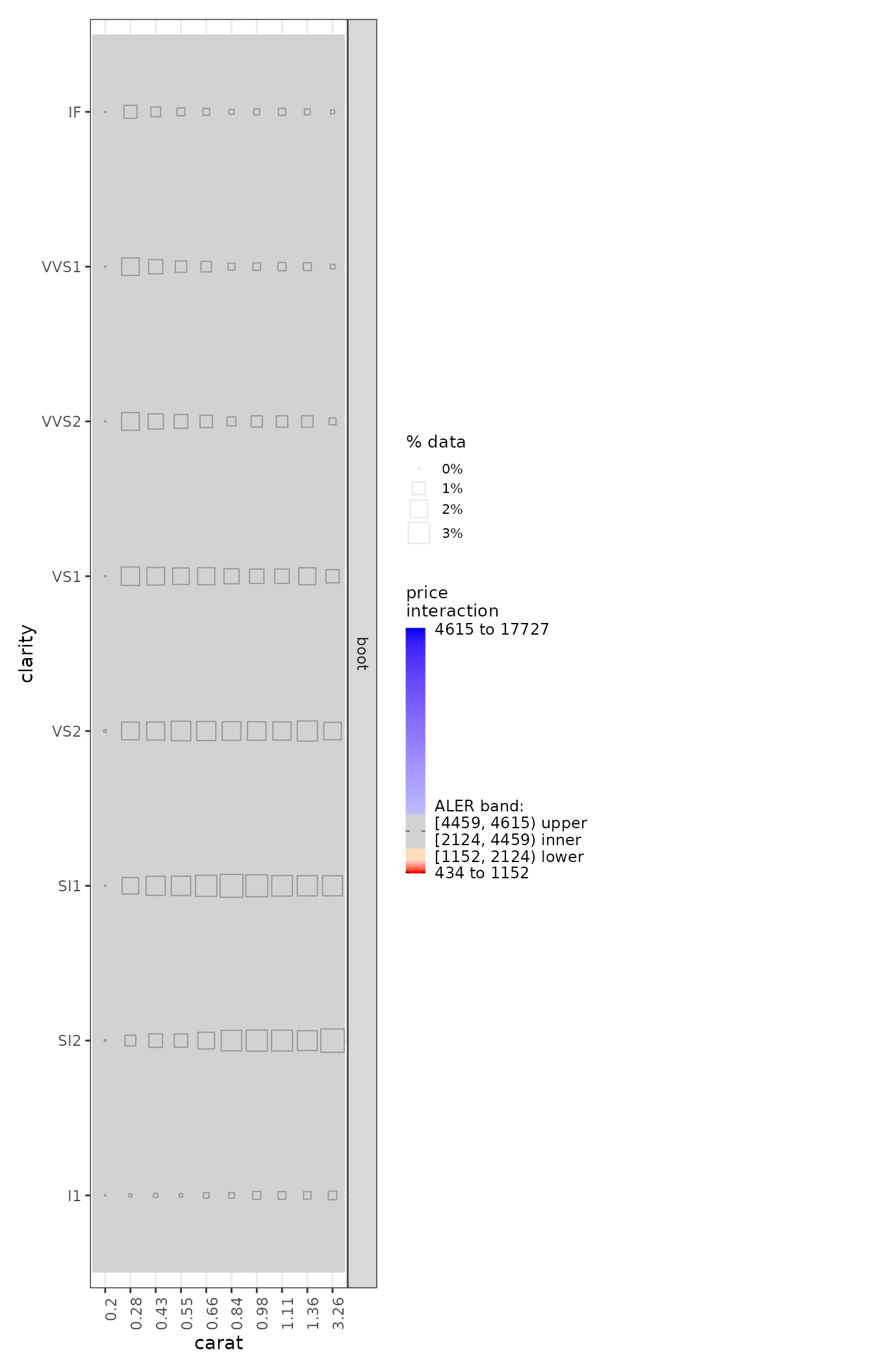
In this case, the bootstrapped results are mostly similar to single
(non-bootstrapped) ALE result. In principle, we should always bootstrap
the results and trust only in bootstrapped results. The most unusual
result is that values of x_length (the length of the
diamond) from 6.2 mm or so and higher are associated with lower diamond
prices. When we compare this with the y_width value (width
of the diamond), we suspect that when both the length and width (that
is, the size) of a diamond become increasingly large, the price
increases so much more rapidly with the width than with the length that
the width has an inordinately high effect that is tempered by a
decreased effect of the length at those high values. This would be worth
further exploration for real analysis, but here we are just introducing
the key features of the package.
ALE interactions
Another advantage of ALE is that it provides data for two-way
interactions between variables. This is also implemented with the
ale() function. When the complete_d argument
is set to 2, then if no variables are specified for
x_cols, ale() generates ALE data on all
possible pairs of input variables used for the model. To change the
default options (e.g., to calculate interactions for only certain pairs
of variables), see details in the help file for the function:
help(ale).
# ALE two-way interactions
ale_2D_gam_diamonds <- ale(
diamonds, gam_diamonds,
complete_d = 2,
parallel = 0 # CRAN limit (delete this line on your own computer)
)The plot() method similarly creates 2D ALE plots from
the ale object. However, the structure is slightly more
complex because of the two levels of interacting variables in the output
data. As before, we first create plots from the ale object
and then we extract the 2D plots from this ale_plots
object:
# Extract two-way ALE plots from the ale_plots object
diamonds_2D_plots <- plot(ale_2D_gam_diamonds)
diamonds_2D_plots <- diamonds_2D_plots$distinct$price$plots[[2]]Because of the 2D interactions, this diamonds_2D_plots
is a two-level list of the 2D ALE plots: the first level is the first
variable in the interaction and the second level is a list of the
interacting variables. So, we use the purrr package to
iterate the list structure to print the 2D plots.
purrr::walk() takes a list as its first argument and then
we specify an anonymous function for what we want to do with each
element of the list. We specify the anonymous function as
\(it.x1) {...} where it.x1 in our case
represents each individual element of diamonds_2D_plots in
turn, that is, a sublist of plots with which the x1 variable interacts.
We print the plots of all the x1 interactions as a combined grid of
plots with patchwork::wrap_plots(), as before.
# Print all interaction plots
diamonds_2D_plots |>
# extract list of x1 ALE interactions groups
purrr::walk(\(it.x1) {
# plot all x2 plots in each it.x1 element
patchwork::wrap_plots(it.x1, ncol = 2) |>
print()
})
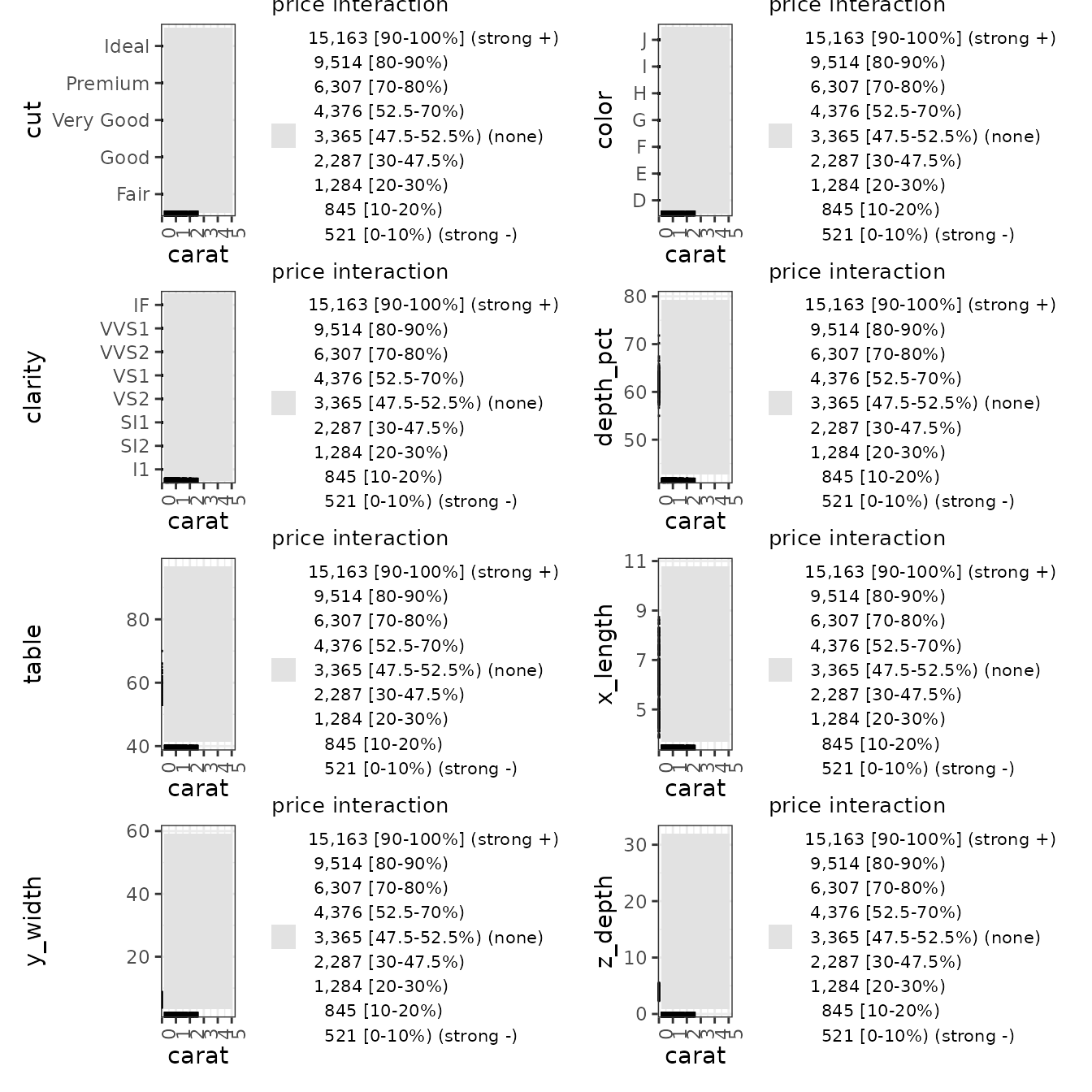
Because we are printing all plots together with the same
patchwork::wrap_plots() statement, some of them might
appear vertically distorted because each plot is forced to be of the
same height. For more fine-tuned presentation, we would need to refer to
a specific plot. For example, we can print the interaction plot between
carat and depth by referring to it thus:
diamonds_2D_plots$carat$depth.
diamonds_2D_plots$carat$depth
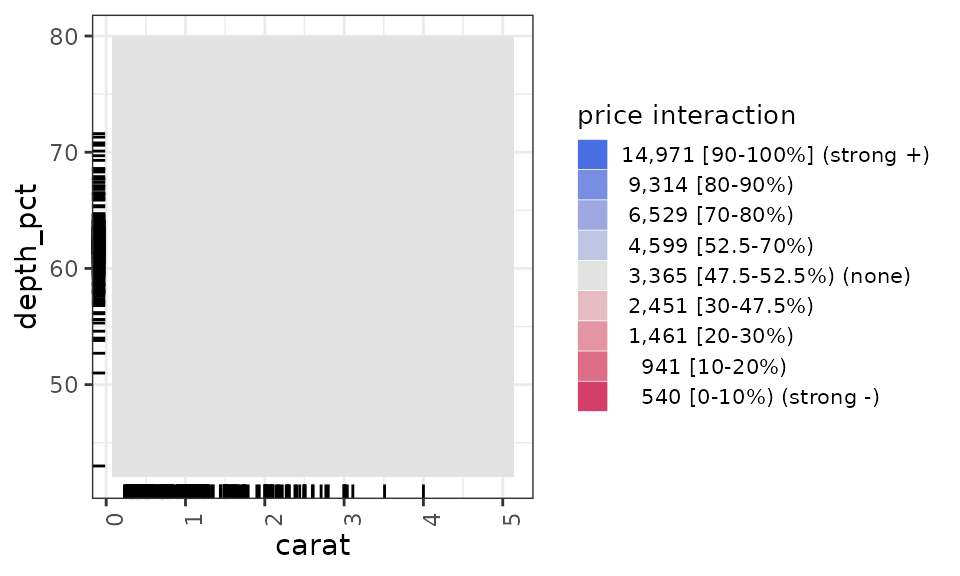
This is not the best dataset to use to illustrate ALE interactions because there are none here. This is expressed in the graphs by the ALE y values all falling in the middle grey band (the median band), which indicates that any interactions would not shift the price outside the middle 5% of its values. In other words, there is no meaningful interaction effect.
Note that ALE interactions are very particular: an ALE interaction
means that two variables have a composite effect over and above their
separate independent effects. So, of course x_length and
y_width both have effects on the price, as the one-way ALE
plots show, but they have no additional composite effect. To see what
ALE interaction plots look like in the presence of interactions, see the
ALEPlot
comparison vignette, which explains the interaction plots in more
detail.